Derivada De Lagrange
Resolviendo para y en las primeras tres ecuaciones de arriba obtenemos Ah qué hermosa simetría. Suponer rgx 0 6 0.
Bienvenidos Al Blog Del Proyecto La Ciencia Es Facil Formulario Basico De Derivacion
Si se cumple que 1 es continua en.

Derivada de lagrange. Se resuelven derivando y llamando y p con lo que obtenemos. UˆRnR funciones C1 con valores reales dados. Em outras palavras encontre os pontos críticos de.
Notaciones de Lagrange y o fx Son de la forma y x fy gy donde fy no puede ser igual y. Sea una función en varias variables y sea una restricción sobre estas variables. El lagrangiano con respecto a esta función y la constricción de arriba es Ahora resolvemos para al hacer cada derivada parcial de esta expresión igual a.
En cálculo diferencial el teorema de valor medio de Lagrange o teorema de Bonnet-Lagrange es una propiedad de las funciones derivables en un intervalo. Se resuelven derivando y llamando y p con lo que obtenemos p fp x fp gpp esta ecuación es lineal y se integra tomando x como función de p. O Teorema de Lagrange também conhecido como Teorema do Valor Médio permite afirmar que numa função contínua e diferenciável num determinado intervalo existe um ponto onde a derivada desse ponto é igual à taxa média de variação da função nesse intervalo.
O método de interpolação descrito nessa seção foi desenvolvido por Joseph Louis de Lagrange motivo pelo qual o método é conhecido por Interpolação de Lagrange. A b R derivable en el intervalo abierto ab a b. Si en lugar de una función tenemos una ecuación como también podemos escribir para representar la derivada.
En la notación de Lagrange la derivada de se expresa como se pronuncia f prima. Esta notación es probablemente la más común cuando se trabaja con funciones de una variable. Consideramos una variable auxiliar y.
Si fj sf restringida a s tiene un m aximo o un m nimo local en S en x 0 entonces existe un numer o real tal que rfx. Ab R f. Sea la función continua f.
Funciones de Rnen R 5 Teorema 1. Supongamos que tuviéramos la curva solución de la ecuación diferencial y trazamos la recta tangente a la curva en el punto dado por la condición inicial. De esta forma definimos el Método de los Multiplicadores de Lagrange de la siguiente forma.
La ecuación de Lagrange correspondiente a la coordenada generalizada qi es d dt L qi L qi 0 i 123. O único polinômio de grau 2 que passa exatamente por todos esses pontos é. Consideremos una partícula que se mueve en el plano OXY estando su posición expresada en coordenadas polares de manera que.
Essa função é chamada de lagrangeana e a nova variável é conhecida como um multiplicador de Lagrange. En los problemas de optimización el método de los multiplicadores de Lagrange llamados así en honor a Joseph Louis Lagrange es un procedimiento para encontrar los máximos y mínimos de funciones de múltiples variables sujetas a restricciones. Enunciado del Teorema El teorema dice lo siguiente.
Teorema del Valor Medio de Lagrange. Fcfb-fab-a Se observarem com atenção a imagem que se. El punto encima de la letra q significa derivada con respecto del tiempo.
Na notação de Lagrange a derivada em relação a x de uma função F x é denotada f x ou fx x em caso de ambiguidade da variável implicada pela derivação. P fp x fp. Teorema de Lagrange o del valor medio Joseph Louis Lagrange 1736 - 1813 Si fx es continua en el intervalo cerrado ab y derivable en todo punto del intervalo abierto ab entonces existe al menos un punto c donde fc fb - fab - a.
2 es derivablel en existe la deivara para todo punto dentro de. La idea del método de Euler es muy sencilla y está basada en el significado geométrico de la derivada de una función en un punto dado. M etodo de los multiplicadores de lagrange.
Esto sin embargo es menos común. A notação de Lagrange é por vezes incorretamente atribuída a Newton. Introduza uma nova variável e defina uma nova função como a seguir.
-x22x6 x2 2x 6. Y xϕ y ψ y0. Notaciones de Lagrange y o fx Son de la forma y x fy gy donde fy no puede ser igual y.
Mostraremos la potencia y sencillez de la formulación de Lagrange Si T es la energía cinética y V la potencial entonces la lagrangiana LT-V. Em linguagem matemática equivale a afirmar o seguinte. Iguale o gradiente de ao vetor nulo.
Para calcular los puntos críticos de esta función. Las ecuaciones de Lagrange proporcionan un método para calcular las componentes de la aceleración en diferentes sistemas de coordenadas sin tener que complicarse con vectores de la base y sus derivadas. Recuerda hacer la derivada parcial con respecto a igual a solo reitera la constricción.
Lagrange fue un matemático muy prodigioso realizó múltiples contribuciones a el desarrollo del cálculo diferencial e integral La llamada notación de Lagrange es simplemente la enunciación de una función que depende de una o varias variables y se ha derivado sin importar cuantas veces se derive la función la notación no cambia notoriamente es por ejemplo. Sean x 0 2uy gx 0 c y sea Sel conjunto de nivel de gcon valor c. Sea una función real.
F b f a f cba f b f a f c b a Se puede demostrar aplicando el teorema de Rolle a la función. Explicación de un problema para obtener las derivadas numéricas empleando polinomios de Lagrange de grado 1 y 2. Entonces c ab c a b tal que.
Inge Darwin Instagram Facebook

Multiplicadores De Lagrange Paso A Paso Calculo Multivariable Youtube

Derivacion Numerica Mediante Polinomios De Lagrange Youtube

Multiplicadores De Lagrange Ejemplos 1 Y 2 Youtube

201 Notacion De La Derivada Profe Chuy Youtube

Teorema De Lagrange Fuentes De Energia En El Peru

8 La Funcion Derivada Derivadas Ppt Video Online Descargar
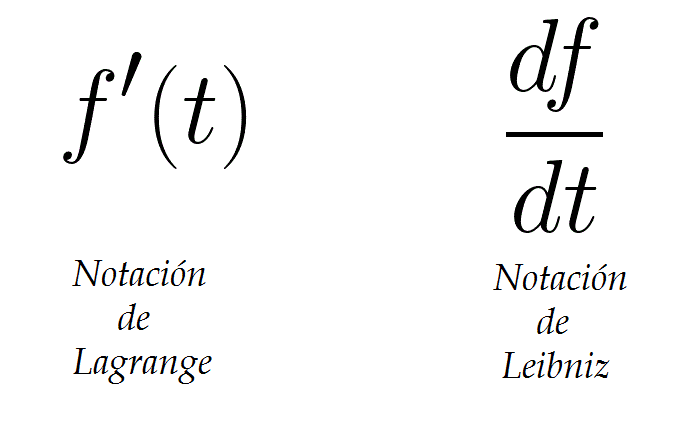
Derivadas Con Primas O Con Diferenciales Fuga De Cerebros
Que Es La Notacion De Lagrange Quora

Multiplicadores De Lagrange Valores Extremos De Las Funciones F X Y La Prof Lina M3 Youtube

Historia De Las Notaciones Para Derivacion Ecuaciones Diferenciales

Multiplicadores De Lagrange Como Funcionan Youtube
2 8 Maximos Y Minimos Con Restricciones Y Multiplicadores De Lagrange Instituto De Geogebra Calculo 3

4 6 Optimizacion Con Restriccion Matriz Hessiana Multiplicadores De Lagrange Pfm Sierra Exportadora De Papa

Ppt Multiplicadores De Lagrange Powerpoint Presentation Free Download Id 6048226

4 6 Optimizacion Con Restriccion Matriz Hessiana Multiplicadores De Lagrange Pfm Sierra Exportadora De Papa








Post a Comment for "Derivada De Lagrange"