Limites De Funciones Determinados E Indeterminados Polinomiales
Si es un función polinómica de cualquier grado entonces. Solución lim 𝑋2 𝑥 2 𝑥2 4 2 2 22 4 0 0 LIMITES INDETERMINADOS Un límite indeterminado es aquel que al ser evaluado en el punto dado la solución es una indeterminación a0 está indeterminación se da cuando en el denominador el resultado es 0 y es una indeterminación debido que la división por cero no es posible.

Limite De Una Funcion Universo Formulas
Se debe tener en cuenta que el límite de una función polinomial de grado n ³ 1 cuando x tiende a ó a - es ó -.

Limites de funciones determinados e indeterminados polinomiales. En análisis real para funciones de una variable se puede hacer una definición de límite similar a la de límite de una sucesión en la cual los valores que toma la función dentro de un intervalo se van aproximando a un punto fijado c independientemente de que éste pertenezca al dominio de la función. Para una única variable x una función racional se puede escribir como. Cálculo de límites de funciones polinómicas cuando x tiende a un infinito.
Límite de una función. El límite de una función polinomial en el infinito es igual al límite del término de mayor grado. LIMITE DE FUNCIONES INDETERMINADAS 1.
Para demostrar esta afirmación escribimos. Por ello Es decir es toda función polinomial por ser continua para obtener el límite basta con sustituir la. Limites de funciones determinados e indeterminados.
Una función racional es una función de la forma. Sumamos y restamos 1 dentro del paréntesis y después operamos dejando el término 1 despejado. Q x donde P y Q son polinomios y x es una variable indeterminada siendo Q un polinomio no nulo.
La factorización La racionalización y otrasDe. La indeterminacin Para salvar indeterminaciones de este tipo es posible reducir el cociente planteado a otro cuyo denominador no sea cero factorizando el numerador yo el denominador cancelando luego los factores comunes. Hacemos el inverso del inverso de la fracción que nos ha quedado que es lo mismo que pasar el numerador de la fracción como denominador de x2.
Para ello se plantean una serie de ejercicios los cuales serán desarrollados paso a paso resaltando aquellos aspectos importantes para resolver cada uno de ellos. Dada una función polinomial de grado n 0 px a 0 x n a 1 x n-1 a 2 x n-2 a n. CÁLCULO DE LIMITES DE FUNCIONES RACIONALES 10.
Sin embargo hay otros casos en que estamos ante límites indeterminados lo que no significa que el límite no exista o que no se pueda determinar sino que la aplicación de las propiedades de los. Cuando después de evaluar el límite de una función en un punto a se obtiene una forma indeterminada comoSe dice que el límite cuando la función tiende a éste punto es una forma indeterminadaPara poder evaluar el comportamiento de la función en el punto a se debe hacer uso de reglas algebraicas tales como. Cálculo de límites de funciones polinómicas cuando x tiende a un número.
P x f x ------- siendo el grado de. Límite de f x para los valores mas cercanos a xa. Decimos que un límite es indeterminado si al calcularlo el resultado no tiene sentido en R.
Se dividen numerador y denominador entre la mayor potencia de x que aparezca. Rx Px Qx Cálculo de limites de funciones racionales 11. Pero vayamos por partes.
Px a 0 x n a 1 x n-1 a 2 x n-2 a n. Cuando el grado del polinomio del numerador es superior al del denominador el limite es. Determinamos si el límite es una indeterminación del tipo 1.
Límites de Funciones Polinomiales por yayajuaarez. Cálculo de limites de funciones polinomicas 8. Sabemos que el dominio de las Funciones Polinomiales.
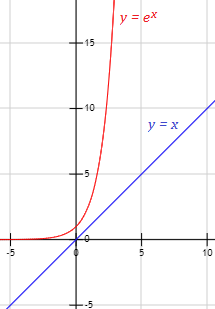
Si c es un número real en el dominio de la función trigonométrica indicada se cumplen los siguientes límites de funciones trigonométricas. El orden del infinito es mayor en e x que en x por tanto el denominador tiende a infinito mucho más rápido que el numerador. Si al evaluar el límite una función racional del tipo fx gx hx por sustitución directa obtenemos una indeterminación del tipo 0 0 para eliminarla seguimos los siguientes pasos.
Las funciones trigonomtricas surgen de una forma natural al estudiar el tringulo rectngulo y observar que las razones cocientes entre las longitudes de dos cualesquiera de sus lados slo dependen del valor de los ngulos del tringulo. TABLA DE CONTENIDO Límites indeterminados. Si hay raíces en.
Es decir basta con sustituir por para calcular el límite. Es el valor al que se acerca la función para cuando se toman valores de x lo mas próximos posibles a. Cálculo de límites de funciones.
Vídeo sobre el cálculo de límites de funciones polinomiales About Press Copyright Contact us Creators Advertise Developers Terms Privacy Policy Safety How YouTube works Test new. En el estudio de los límites de funciones racionales. Publicado por sergioramirez183d en 5 septiembre 2013 en Tareas y avisos de representacion simbolica y.
Donde lim es la manera abreviada de escribir límite x a se lee cuando x tiende al valor a en la función es decir cuando la variable x toma valores muy cercanos al valor a y L es el resultado del límite. Cálculo de limites de funciones polinomicas Ejemplos. Límite de funciones racionales.
Si es un función polinómica de cualquier grado entonces. Límite de una función polinomial. Lmites de funciones determinadas e indeterminadas Trigonomtricas.
Es el conjunto de los números reales es decir para todo valor de x en la recta numéricaexiste un valor definido de f x de lo que la hace continua en cualquier valor de x. En análisis real para funciones de una variable se puede hacer una definición de límite similar a la de límite de una sucesión en la cual los valores que toma la función dentro de un intervalo se van aproximando a un punto fijado c independientemente de que éste pertenezca al dominio de la función. Una función racional es el cociente de dos polinomios.
Límites infinitos 3. La expresión general de un límite es la siguiente. CALCULO DE LÍMITES DETERMINADOS.
Las funciones racionales son funciones obtenidas al dividir un polinomio por otro polinomio distinto de cero. LIMITES INDETERMINADOS E INFINITOS 2. Es decir solo se toma en cuenta el término de mayor grado.
En otras ocasiones es posible crear un factor comn multiplicando el numerador y el denominador por la expresin. El límite de una función y f x para la variable x a a la expresión. Son los valores que toma una función dentro de un intervalo que se van aproximando a un punto fijo c.
Se factorizan numerador y denominador. Para resolver límites de este tipo se dividen el numerador y el denominador de la función dada por x n siendo n el mayor de los grados de las funciones polinomiales. Comprobar la indeterminación Aplicamos sustitución directa.
Es importante recalcar que este tema es de suma importancia para el cálculo de límites. Como a0 podemos asegurar que. Se dice que el límite de la función f x es L cuando x tiende a c y se escribe.
Luego se aplican las propiedades de los límites. Solución lim 𝑋2 𝑥 2 𝑥2 4 2 2 22 4 0 0 LIMITES INDETERMINADOS Un límite indeterminado es aquel que al ser evaluado en el punto dado la solución es una.

Limite De Una Funcion Universo Formulas
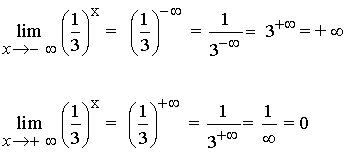
Resumen De Todos Los Limites Determinados E Indeterminados Ejemplos Resueltos
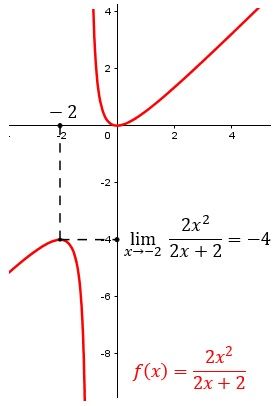
Limite De Una Funcion Universo Formulas
Limites De Funciones Polinomicas Y Racionales Ck 12 Foundation

Limites Algebraicos Ejercicio 8 Youtube
Limites De Funciones Determinadas E Indeterminadas Pdf Funcion Continua Logaritmo

Limites Trigonometricos Indeterminados Ejercicios Resueltos Fisimat Limites Trigonometricos Calculo De Limites Formulas Matematicas

Limites De Funciones Racionales Con Radicales Youtube

Limite De Una Funcion Universo Formulas
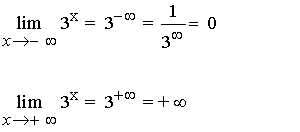
Resumen De Todos Los Limites Determinados E Indeterminados Ejemplos Resueltos

Limite De Una Funcion Universo Formulas

Limites De Funciones Potencias Y Numero E Bachillerato Youtube

Limite De Funciones Racionales Miprofe Com
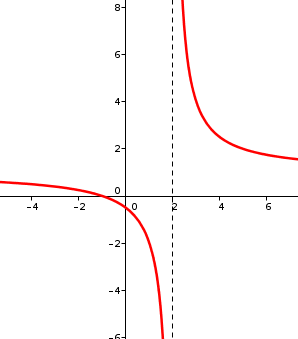
Calculo De Limites De Funciones Racionales Ii Matematicas Ies
Calculo De Limites Paso A Paso

Limite De Una Funcion Universo Formulas
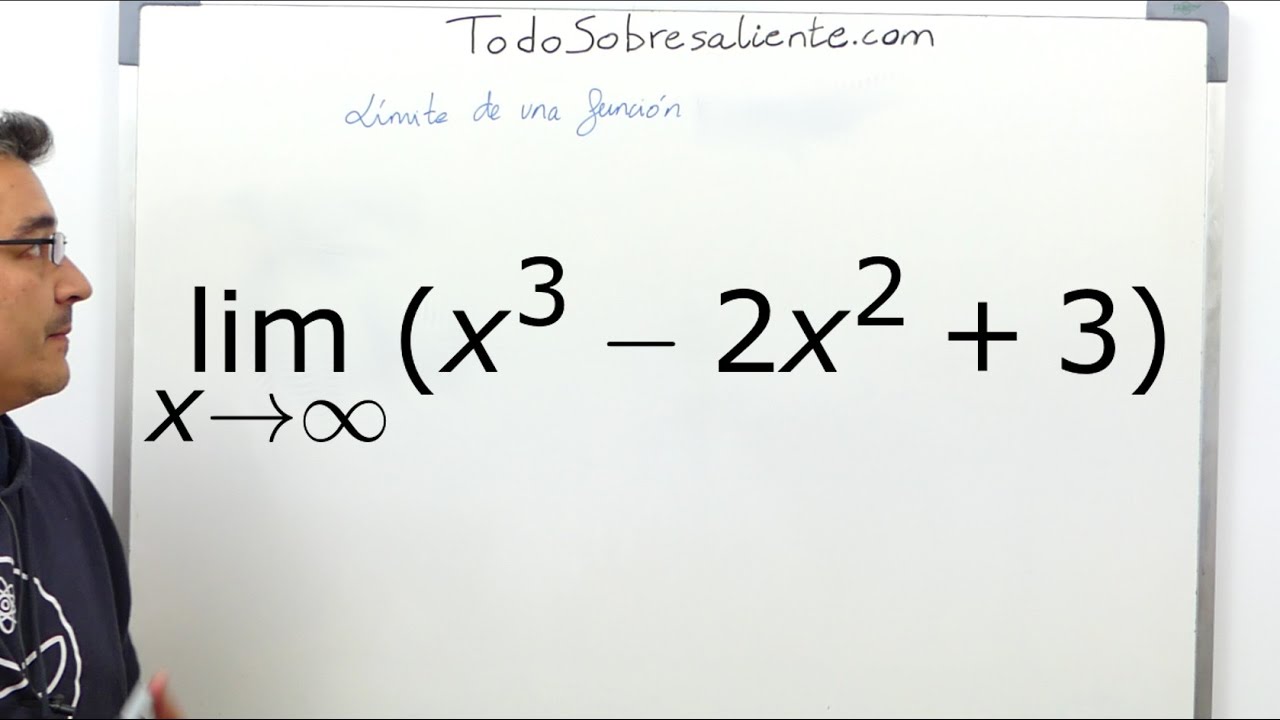
Limite De Una Funcion En El Infinito Funciones Polinomicas Youtube

Limite De Una Funcion Universo Formulas







Post a Comment for "Limites De Funciones Determinados E Indeterminados Polinomiales"